متاسفانه نظرتان اشتباه است.در تئوری ام آن چه مطرح می شود 10 بعد مکان و 1بعد زمان است.در زمان بیگ بنگ 10 بعد مکانی بودند و 1بعد زمان مشترک در هر ده بعد آمیخته (نسبیت عام).در ضمن آنچه که شما از آن به ابعاد یاد کردید در واقع 4 نیروی عامل جهان و متغیر های ابعاد هستند.)g=t(هستند همچنین ضد ماده و ماده ی تاریک هم از این نیرو ها اشتقاق می یابند.منظور من از این سوال چگونگی چیدمان این بعد ها از لحاظ ریاضیات بود.4 بعد اول از نظر ریاضیات 3 بردار یکه (i,j,k)بعد زمان در این سه آمیخته است.در زمان بیگ بنگ هنگامی که 11 بعد در هم دوخته پس از انفجار دو تکه جهان موازی که یکی جهان 3 بعدی ما و دیگری جهان 7 بعدی است که زمان در این میان اشتراک داردبه وجود آمد.با استفاده از ریاضیات پیش بینی می شود که در اولین بعد از جهان دیگر جنبه منفی زمان (جنبه ی مختلط و موهومی اعداد )باید ظاهر شود.یعنی زمان منفی است.اگر این طور باشد طبق رابطه تبدیلاتی زمان از نسبیت خاص در تبدیلات لورنتس که مخرج کسر

است اگر زمان منفی شود حاصل درون رادیکال منفی خواهد بود.((اگر با مکانیک موجی آشنایی دارید (

)منظورم را متوجه می شوید)).یعنی نسبت سرعت شخص به سرعت نور از 1 بزرگتر و در نتیجه سرعت شخص از سرعت نور بیشتر می تواند شود.این نسبیت را نقض نمی کند چون خود اینشتین باور داشت که در چهار بعد حداکثر سرعت سرعت نور است و نه در بعد پنجم مکانی .منظور من از این سوال توضیح ابعاد نبود چگونگی معادلات مختصاتی آن ها در ریاضیات بود.ولی به هر حال از (مخفی) متشکرم.





 پاسخ با نقل قول
پاسخ با نقل قول






 .منظورم از تعریف بعد x ، یک تعریف بدون وابستگی به سایر بعدهاست.
.منظورم از تعریف بعد x ، یک تعریف بدون وابستگی به سایر بعدهاست.
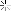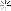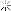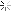


علاقه مندی ها (Bookmarks)