مقدمه و معرفی
شاید تابه حال فرایندهای زیادی را دیده باشید که طی آن دو چیز با هم ترکیب میشوند و شی سوم متمایزی را حاصل می دهند. مثلاً تصور کنید در یک کلاس درس معلم کلاس میگوید "ب"، "آ" و دانش آموزان باهم فریاد میزنند "با". این بار معلم میگوید "ب"، "و" و اینبار دانشآموزان فریاد میزنند "بو". و یا در مثالی دیگر در طبیعت ملکولهای هیدروژن و اکسیژن با هم ترکیب شده و ماده سومی چون آب را پدید میآورد. اینها همگی نمونههایی از اعمالی دوتایی هستند که در طی آنها دو عنصر شرکت کننده شی سومی را پدید میآورند. اعمال دوتایی و به دنبال آن ساختارهای جبری از مهمترین و مقدماتیترین مفاهیم در جبر مجرد هستند. در ادامه به تعریف دقیق یک عمل دوتایی در جبر میپردازیم و ویژگیهای آنها را بررسی میکنیم.
عمل دوتایی
یک عمل دوتایی روی مجموعه ناتهی G تابعی است چوناز G×G به توی G که به هر عضو (a,b) از G×G یک عضو چون C از G را نسبت میدهد. لازم به ذکر است که
. با توجه به تعریف یک عمل دوتایی، یک عمل دوتایی چون * روی یک مجموعه ناتهی G باید واجد شرایط زیرباشد:
اگر * یک عمل دوتایی تعریف شده در مجموعه ناتهی G باشد مینویسم (*,G) برای هر (a,b) عضو G×G حاصل عمل * روی (a,b) را به صورت (a,b)* یا معمولتر به فرم a*b نشان می دهیم و معمولا برای سهولت در نوشتن a*b را به صورت ab مینویسیم. همچنین معمولاً یک عمل دوتایی روی یک مجموعه را با دو نماد جمعی + و ضربی . نشان میدهیم که نباید آنها را با جمع و ضرب اعداد خلط کرد. اگر عمل دوتایی را به فرم جمعی نشان دهیم حاصل عمل + را روی (a,b) به صورت a+b نشان میدهیم و اگر عمل عمل را با نماد ضربی نشان دهیم حاصل عمل را به صورت a.b نشان میدهیم.
- عمل دوتایی روی کل دامنه خود یعنی G×G تعریف شده باشد.
- عمل دوتایی * یک تابع خوشتعریف از G×Gعمل دوتایی به توی G باشد یعنی به هر عضو عنصرG×G کتایی از G را نسبت میدهد.
- حاصل ترکیب دو عضو (a,b) تحت یک عمل دوتایی باید متعلق به G باشد. به عبارت دیگر مجموعه G نسبت به عمل دوتایی خود بسته باشد.
- عمل دوتایی را که سبب ترکیب هر دو عضو مجموعه ناتهی * میشود، معمولا با * یا
نمایش میدهیم.
نمونههایی از اعمال دوتایی
بسته بودن نسبت به یک عمل دوتایی
- مجموعه اعداد صحیح را در نظر بگیرید ،
را به صورت زیر تعریف میکنیم:
به آسانی دیده میشود * یک عمل دوتایی است.
- مجموعه اعداد طبیعی N را در نظر بگیرید. * با ضابطه زیر ، یک عمل دوتایی است:
اما عمل فوق در Z و Q عمل دوتایی نمیباشد.(چرا؟) ولی در R عمل * فوق ، یک عمل دوتایی است.
- عمل * را در مجموعه A به صورت زیر تعریف میکنیم:
عمل * در A=Q یک عمل دوتایی نیست . چرا که به ازای a=b جواب a*b تعریف نشده میشود که متعلق به Q نیست. همچنین است درباره َA=R .
مجموعه اعداد صحیح و عمل جمع اعداد را در نظر بگیرید. عمل جمع اعداد یک عمل دوتایی روی مجموعه اعداد صحیح است و بدیهی است که با توجه به تعریف عمل دوتایی روی Z برای هر دو عدد صحیح a و b عدد a+b نیز عددی صحیح است. حال مجموعه اعداد صحیح زوجکه زیرمجموعهای از Z است را در نظر بگیرید. برای هر دو عضو این مجموعه چون m و n چون مجموع دو عدد زوج عدی زوج است عدد m+n زوج است پس متعلق به مجموعه اعداد صحیح زوج است. به عبارت برای هر
داریم
در این حالت اصطلاحاً میگوییم مجموعه اعداد صحیح زوج تحت عمل جمع بسته است. اما همواره برای هر زیرمجموعه Z چنین نیست. مثلا مجموعه اعداد صحیح فرد
را در نظر بگیرید. مجموعه دو عدد صحیح فرد عددی زوج است که دیگر به مجموعه اعداد صحیح فرد تعلق ندارد پس برای هر
داریم
. در این حالت میگوییم مجموعه اعداد صحیح فرد تحت عمل جمع بسته نمیباشد.
اگر G یک مجموعه ناتهی و * یک عمل دوتایی تعریف شده روی G باشد وگوییم E تحت عمل G بسته است در صورتیکه به ازای هر
داشته باشیم
به عنوان مثال:
.
دوست عزیز، به سایت علمی نخبگان جوان خوش آمدید
مشاهده این پیام به این معنی است که شما در سایت عضو نیستید، لطفا در صورت تمایل جهت عضویت در سایت علمی نخبگان جوان اینجا کلیک کنید.
توجه داشته باشید، در صورتی که عضو سایت نباشید نمی توانید از تمامی امکانات و خدمات سایت استفاده کنید.



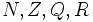 تحت عمل جمع بسته میباشند.
تحت عمل جمع بسته میباشند.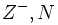 تحت عمل تقسیم بسته نیستند.
تحت عمل تقسیم بسته نیستند.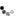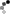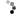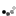
 پاسخ با نقل قول
پاسخ با نقل قول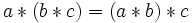 به عنوان مثال:
به عنوان مثال: 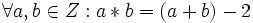 Z تحت عمل * شرکت پذیر است.
Z تحت عمل * شرکت پذیر است.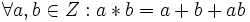 عمل * روی Z خاصیت شرکت پذیری دارد.
عمل * روی Z خاصیت شرکت پذیری دارد. یک نیمگروه است هر گاه عمل * روی G شرکت پذیر باشد. به عنوان مثال:
یک نیمگروه است هر گاه عمل * روی G شرکت پذیر باشد. به عنوان مثال:  و
و 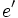 باشد. در این صورت چون
باشد. در این صورت چون 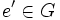 و e عضو خنثی G نسبت به عمل * است داریم
و e عضو خنثی G نسبت به عمل * است داریم 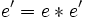 . و چون
. و چون 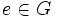 و
و 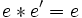 که دو تساوی اخیر نشان می دهد
که دو تساوی اخیر نشان می دهد 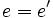 و حکم ثابت می شود.
و حکم ثابت می شود.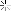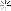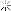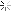


علاقه مندی ها (Bookmarks)