گروه از جمله مهمترین ساختارهای جبری است که نقش اساسی در جبر مجرد دارد و در علوم مختلف مانند بلورشناسی، فیزیک، کوانتوم و... از اهمیت بالایی برخوردار است.
فکر تشکیل نظریه گروهها زمانی شکل گرفت که ریاضیدانان مشاهده کردند ساختارهایی را که مطالعه میکنند در خواصی مشترک هستند و اگر بتوانند همه این خواص را در مورد یک ساختار مشخص بررسی کنند در حقیقت بخش وسیعی از ساختارهای مشابه را مطالعه کردهاند و به این ترتیب در زمان صرفه جویی میشود.
شاخهای از ریاضیات را که به مطالعه گروهها اختصاص دارد نظریه گروهها نامیده میشود.
مرور تاریخی
نظریه گروهها بهوسیله چهارشاخه عمده از ریاضیات جبر کلاسیک، نظریه اعداد، هندسه و آنالیز رشد و گسترش یافت. جبر کلاسیک در سال 1770 با کارهای ژوزف لویی لاگرانژ برروی معادلات چندجملهای پایه گذاری شد.
نظریه اعداد بهوسیله کارل فردریش گاوس در سال 1801 مورد مطالعه و گسترش هرچه بیشتر قرار گرفت و سی.اف.کلاین در زمینه هندسه و ارتباط تبدیلات هندسی و گروهها کارهای بسیار انجام دادهاست به طوری که او را پدر این بخش از نظریه گروهها میدانند و بنیانگذار شاخه آنالیز نیز هنری پوانکاره، اس.لی لای و سی.اف.کلاین هستند.
اما اویلر(Euler)، گاوس(Gauss)، لاگرانژ(Lagrange)، آبل(Abel) و ریاضیدان فرانسوی گالوا(Galois) اولین کسانی بودند که در زمینه نظریه گروهها به تحقیق پرداخته بودند. خصوصاً گالوا بدلیل قضیه اساسی خود که رابطی بین گروهها و حلقهها است و امروزه آن را قضیه گالوا میخوانند بسیار مورد توجه است.
اگرچه مفهوم گروه تبدیلها در مطالعه هندسه به کندی صورت گرفته است، اما کار اصلی در گسترش مغهوم گروه از مطالعه معادلات چندجملهای حاصل شده است. یونانیان قدیم از روشهای حل معادله درجه دو آگاه بودند. در قرن شانزدهم قدمهایی برای حل معادلات درجه سوم و چهارم روی Q برداشته شد. اولین کاربرد گروهها در توصیف تأثیر جایگشتهای ریشههای یک معادله چند جملهای بودهاست که بهوسیله لاگرانژ مورد استفاده قرار گرفتهاست که بر مبنای همین او توانست نظریه جانشانی را سازمان دهد.
او کشف کرد که ریشههای همه مواردی را که او امتحان کردهاست توابعی گویا از ریشههای معادلات متناظرشان هستند. لئونارد اویلر(1707-1783) و ژوزف لویی لاگرانژ(1736-1813) هر دو، با ادامه کار با چند جمله ایهای درجه پجم و بالاتر سعی کردند معادله درجه پنجم کلی را حل کنند. لاگرانژ دریافته بود که بین درجه n معادله چند جملهای و گروه جایگشتی Sn باید رابطهای وجود داشته باشد. پس از او رافینی در تلاش برای اثبات عدم وجود راه حل مستقیم برای حل معادلات درجه پنجم و بالاتر گامهای دیگری را در زمینه نظریه گروهها برداشت.
اما این نیلس هنری آبل(1802-1829) بود که سرانجام ثابت کرد پیدا کردن فرمولی برای حل معادله درجه پنجم کلی، تنها با جمع و تفریق و ضرب و تقسیم و ریشه گیری ممکن نیست.
در طی همین دوران، اواریست گالوا (1811-1832) ریاضیدان معروف فرانسوی وجود شرط لازم و کافی برای حل چند جملهای درجه پپنجم یا بالاتر با ضرایب گویا، به وسیله رادیکالها را تحقیق کرد. در کار گالوا ساختارهای گروهی و هیاتها به کار میروند.گالوا نخستین اثر خود را در مورد نظریه گروهها در سن 18 سالگی(1829)منتشر ساخت. اما کمکهای او تا قبل از انتشار مجموعه مقالاتش در سال 1846 مورد توجه قرار نگرفت.
به دنبال دستاوردهای گالوا، نظریه گروهها جای خود را در بسیاری از زمینههای ریاضی باز کرد. مثلا، ریاضی دان آلمانی فلیکس کلاین (1849-1929) در آنچه که به برنامه ارلانگر معروف است، سعی کرد که تمام هندسههای موجود را بر حسب گروه تبدیلهایی که تحت آنها ویژگیهای هندسه ناوردا بودند تدوین کند.
بعد از او آرتور کیلی و آگوشتین لوی کوشی به اهمیت کارهای گالوا پی بردند و به تحقیقات بیشتر در این زمینه پرداختند. از جمله ریاضیدانانی که در قرن نوزدهم در زمینه نظریه گروهها کار میکردند میتوان برتراند، چارلز هرمیت، فروبنیوس و لئوپارد کرونکر و امیل ماتیو را نام برد.
تا آن زمان اصول موضوع معینی برای تعریف گروه وجود نداشت. در سال 1854 کیلی اولین اصول موضوع را برای گروهها ارائه داد اما تعریف وی به زودی فاقد ارزش شد. در سال 1870، کرونکر مجدداً اصول موضوعی را برای گروهها پایه گذاشت. همچنین اچ.وبر در سال 1882، تعریفی برای گروه های متناهی و در سال 1883 تعریفی برای گروههای نامتناهی انجام داد.
والتر فون دایک در سال 1882 اولین تعریف مدرن از گروه را ارائه داد.
مطالعه گروه های لای و زیرگروه های گسسته شان و گروههای تبدیلی در سال 1884 به طور منظم توسط سوفوس لای شورع شد.
در طی قرن بیستم پژوهشهای بسیار زیادی برای تحلیل ساختار گروههای متناهی صورت گرفت. در دهههای اخیر، ریاضیدانان در جست و جوی همه گروههای ساده متناهی و توضیح نقش آنها در ساختار تمام گروههای متناهی بودهاند. از جمله پشگامان این بسط، والتر فیت، جان تامسون، دانیل گورنشتین، می شاییل آشباختر و رابرت گریس هستند.
امروزه نظریه گروهها به بنیادیترین نظریهها در جبر مجرد تبدیل شدهاست و منبع تحقیقات فراوانی برای ریاضیدانان است.
ویکی پدیا
دوست عزیز، به سایت علمی نخبگان جوان خوش آمدید
مشاهده این پیام به این معنی است که شما در سایت عضو نیستید، لطفا در صورت تمایل جهت عضویت در سایت علمی نخبگان جوان اینجا کلیک کنید.
توجه داشته باشید، در صورتی که عضو سایت نباشید نمی توانید از تمامی امکانات و خدمات سایت استفاده کنید.



.gif)
 پاسخ با نقل قول
پاسخ با نقل قول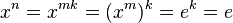
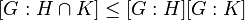
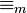 یک رابطه هم ارزی روی مجموعه اعداد صحبح
یک رابطه هم ارزی روی مجموعه اعداد صحبح  تعریف میکند
تعریف میکند  نشان میدهیم.
نشان میدهیم.  نشان دهیم،
نشان دهیم،  حال عمل ⊕ موسوم به جمع نیمی یا جمع با پیمانه m را به صورت
حال عمل ⊕ موسوم به جمع نیمی یا جمع با پیمانه m را به صورت تعریف میکنیم. در این صورت خواننده آشنا با نظریه همنهشتی به سادگی میتواند بررسی کند که
تعریف میکنیم. در این صورت خواننده آشنا با نظریه همنهشتی به سادگی میتواند بررسی کند که 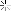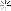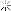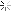


علاقه مندی ها (Bookmarks)