:::::من این پست را واسه تنوع گذاشتم::::
عشق تابعی است
که وقتی متغیر ان
به سمت خدا میل کند
حدش به بینهایت میرسد
دوست عزیز، به سایت علمی نخبگان جوان خوش آمدید
مشاهده این پیام به این معنی است که شما در سایت عضو نیستید، لطفا در صورت تمایل جهت عضویت در سایت علمی نخبگان جوان اینجا کلیک کنید.
توجه داشته باشید، در صورتی که عضو سایت نباشید نمی توانید از تمامی امکانات و خدمات سایت استفاده کنید.



.gif)

 پاسخ با نقل قول
پاسخ با نقل قول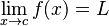
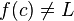 باشد. در حقیقت حتی نیازی نیست که
باشد. در حقیقت حتی نیازی نیست که 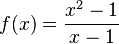
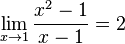


 بوده باشد. کشف این عدد منتسب به فیثاغورسیان (شاگردان
بوده باشد. کشف این عدد منتسب به فیثاغورسیان (شاگردان 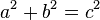 بدست میآید. در ریاضیات کلاسیک هم
بدست میآید. در ریاضیات کلاسیک هم 


علاقه مندی ها (Bookmarks)